💜 하노이의 탑이란?
1) 정의
- 하노이의 탑은 퍼즐의 일종으로, 세 개의 기둥과 이 기둥에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있다.

2) 조건
- 한 번에 한개의 원판만 옮길 수 있다.
- 가장 위에 있는 원판만 이동할 수 있다.
- 큰 원판이 작은 원판 위에 있어서는 안 된다
3) 목표
- 세 막대를 왼쪽부터 A, B, C라고 가정하자.
- 위 조건에 맞게 모든 원판을 A에서 C로 옮겨야 한다.

💜 어떤 기능을 하는 함수를 구현해야하는가? (문제 정의)
- 원반의 이동 횟수를 최소화한다.
- 각 원반을 옮기는 모든 순서를 출력한다.
=> 원반 개수 N개를 입력 받아, 모든 원반을 C막대에 옮기는 모든 과정을 출력한다.
💜 문제를 어떻게 해결할 것인가? (아이디어 얻기)
- 원반의 개수에 따라 알고리즘이 더 복잡해진다.
- 원반의 개수가 최소인 경우를 실제로 해보자! > 원반 3개를 가지고 해보자!
1) 분할정복(Divide and conquer): 큰 문제를 작은 문제로 세분화하여 해결
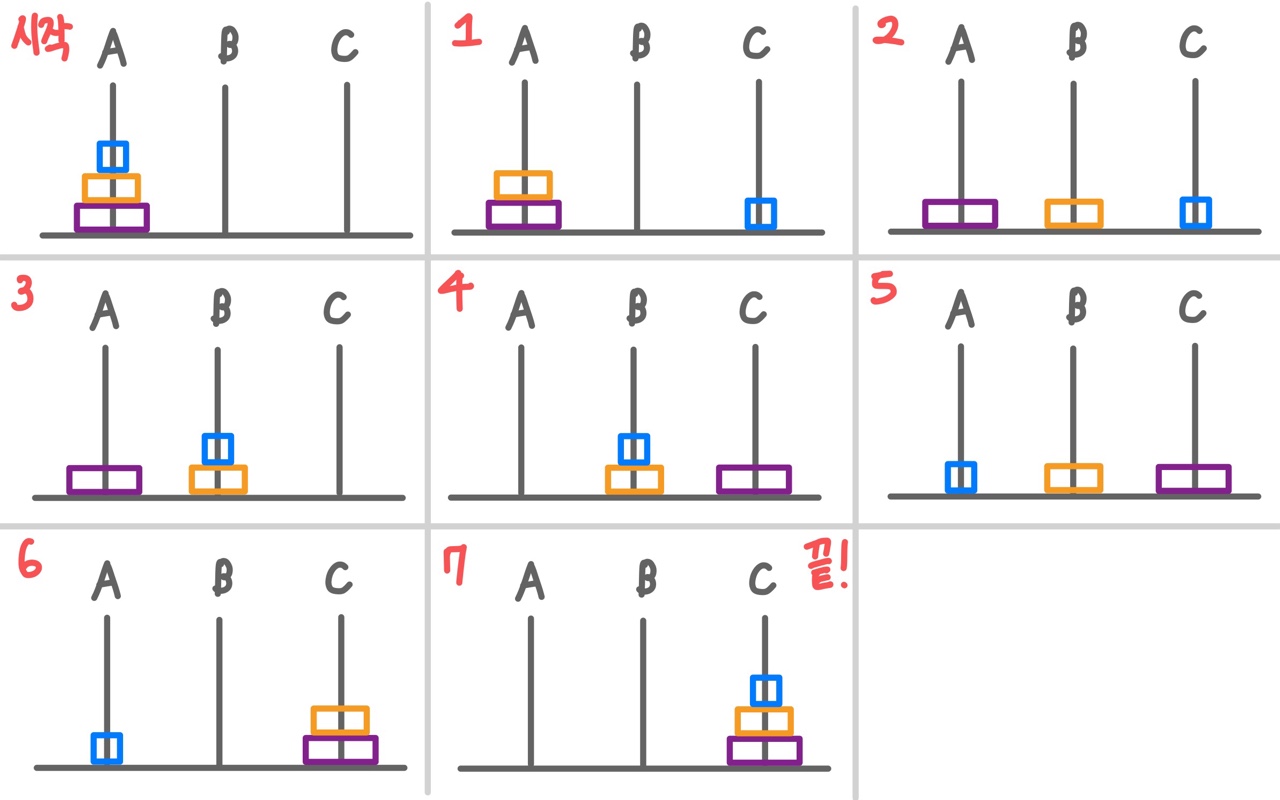
2) 재귀를 활용!
: N-1개의 원판 > 맨 밑에 있는 원판 1개 + 위에 있는 나머지 N-2개의 원판
: 위의 원판이 1이 될 때까지 똑같은 프로세스 반복 > 재귀 필요!
💜 문제 접근하기 (원반 N개로 가정)
- 원반이 n개 있다고 가정한다.
- 원반을 옮길 때는 반드시 막대 3개를 다 거쳐야 한다. (원반이 1개일 때는 해당 X)
[원상태]
: 맨 밑의 원반 1개, 그 위의 원반 n-1개를 한 묶음으로 본다.

[1단계]
: N-1개의 원판을 A > B 로 옮긴다. (실제 코드 구현 시, A > C > B 순)

[2단계]
: 맨 밑의 원판 1개를 A > C로 옮긴다.

[3단계]
: N-1개의 원판을 B > C 로 옮긴다. (실제 코드 구현 시, B > A > C 순)

💜 실제 코드 & 분석
// 하노이의 탑
// n개의 원판을 by(중간)을 거쳐서 from(처음)에서 to(목표)로 이동
void tower_of_hanoi(int n, char from, char by, char to) {
// 종료 조건: 옮겨야 하는 원판의 수가 1개일 때! > 그냥 옮기면 됨.
if (n == 1) {
printf("원판 1개를 %2c -> %2c로 이동하였습니다.\n", from, to);
}
else {
// 원판 n-1개를 (맨 아래 제외) a -> b로 이동 => 중간 이동!
// [1단계]
tower_of_hanoi(n - 1, from, to, by); // from > to > by (from에서 to를 거쳐서 중간인 by로 이동)
// 큰 원판 1개 (맨아래)를 from에서 to로 이동
// [2단계]
printf("원판 1개를 %2c -> %2c로 이동하였습니다.\n", from, to);
// 원판 n-1개 (1단계에서 옮겨진 원판)를 by에서 from을 거쳐서 to로 이동
// [3단계]
tower_of_hanoi(n - 1, by, from, to);
}
}
5. 참고자료
- 하노이의 탑 - 위키백과: https://ko.wikipedia.org/wiki/%ED%95%98%EB%85%B8%EC%9D%B4%EC%9D%98_%ED%83%91
- '하노이의 탑' 이해하기 (feat.재귀함수) - mgyo: https://mgyo.tistory.com/185
'Algorithm' 카테고리의 다른 글
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2023.10.19 |
|---|---|
| [알고리즘] 너비 우선 탐색(BFS)과 깊이 우선 탐색(DFS) (0) | 2023.10.03 |
| [알고리즘] Greedy Algorithm (탐욕 알고리즘) (0) | 2023.09.26 |
| [알고리즘] Dynamic Programming(동적 계획법) (0) | 2023.09.22 |
| [Algorithm] 8퀸 문제 알고리즘 (재귀) (0) | 2023.08.13 |




댓글